4259. Minimum in the stack
Implement a data
structure with the next operations:
1. Push x to the end of the structure.
2. Pop the last
element from the structure.
3. Print the minimum
element in the structure.

Input. The first line contains the number of operations n (1 ≤ n
≤ 106). Each of the next n lines contains one operation. The i-th line contains the number ti – the type
of operation:
·
1 in the case of a push operation;
·
2 in the case of a pop operation;
·
3 if the operation asks to find the minimum;
In the case of a push operation, next comes the
integer x (-109
≤ x ≤ 109) – element to
be inserted into the structure. It is guaranteed that before each pop
or getMin
operation the structure is not empty.
Output. For each getMin
operation, print on a separate line one number – the minimal element in the
structure.
|
Sample
input |
Sample
output |
|
8 1 2 1 3 1 -3 3 2 3 2 3 |
-3 2 2 |
SOLUTION
stack
Algorithm analysis
Obviously, the
required data structure is the stack.
Since the number n of operations with stack is no more than 106, we will choose a static array of the
specified length as its container.
The pop() method will be modeled as usual
by removing the top element of the stack, and the push(x) method will be rewritten as follows:
·
If the stack is empty, push x to the stack;
·
Otherwise, push to the stack the minimum between x and the current value of its top.
Thus, the
minimum element of the stack will always be at the top. At the same time, we
lose the values pushed onto the stack, although in reality they are not needed
for further requests.
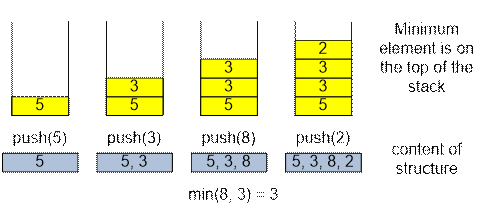
When we process number 8, we push min (8, 3) = 3 at the top of the stack.
Algorithm realization
Declare the class Stack and its methods.
class Stack {
public:
Stack(int
size);
void push(int x);
void pop();
int getMin();
private:
int* m;
int size;
};
Stack::Stack(int size = 1000001) {
m = new int[size];
this->size
= 0;
}
void Stack::push(int
x) {
if (size ==
0)
m[size++] = x;
else
{
int pos =
size - 1;
m[size++] = min(x,m[pos]);
}
}
void Stack::pop() {
size--;
}
int Stack::getMin() {
return
m[size-1];
}
The main part of the program. Simulate the stack.
Stack s;
scanf("%d",&n);
while(n--)
{
scanf("%d",&op);
if (op == 1)
{
scanf("%d",&x);
s.push(x);
} else
if (op == 2)
{
s.pop();
} else
{
printf("%d\n",s.getMin());
}
}
Algorithm realization –
Stack STL
Declare a stack.
stack<int> s;
Read the number of operations n.
scanf("%d",&n);
while(n--)
{
Read the type of operation op.
scanf("%d",&op);
if (op == 1)
{
Add the number x to the stack.
scanf("%d",&x);
if
(s.empty())
s.push(x);
else
s.push(min(s.top(),x));
} else
if (op == 2)
{
Remove a number from the stack.
s.pop();
} else
{
Print the minimum in the structure. It is at the top of the stack.
printf("%d\n",s.top());
}
}
Java realization –
Scannner
import java.util.*;
//import java.io.*;
public class Main
{
public static void
main(String[] args) // throws IOException
{
Scanner con = new
Scanner(System.in);
//Scanner
con = new Scanner(new FileReader ("4259.in"));
Stack<Integer> s = new
Stack<Integer>();
int n = con.nextInt();
while(n--
> 0)
{
int op = con.nextInt();
if (op ==
1)
{
int x = con.nextInt();
if (s.empty())
s.push(x);
else
s.push(Math.min(s.peek(),x));
} else
if (op ==
2)
{
s.pop();
} else
{
System.out.println(s.peek());
}
}
con.close();
}
}
Java realization
– Fast Scannner
import java.util.*;
import java.io.*;
public class Main
{
public static void
main(String[] args) //throws IOException
{
//FastScanner con = new FastScanner(new
FileReader ("4259.in"));
FastScanner
con =
new FastScanner(new InputStreamReader(System.in));
Stack<Integer> s = new
Stack<Integer>();
int n = con.nextInt();
while(n--
> 0)
{
int op = con.nextInt();
if (op ==
1)
{
int x = con.nextInt();
if (s.empty())
s.push(x);
else
s.push(Math.min(s.peek(),x));
} else
if (op ==
2)
{
s.pop();
} else
{
System.out.println(s.peek());
}
}
}
}
class FastScanner
{
private BufferedReader br;
private StringTokenizer st;
public FastScanner(InputStreamReader reader)
{
br = new BufferedReader(reader);
}
public
String next()
{
while (st == null || !st.hasMoreTokens())
{
try
{
st = new StringTokenizer(br.readLine());
} catch
(Exception e)
{
e.printStackTrace();
}
}
return st.nextToken();
}
public int nextInt()
{
return Integer.parseInt(next());
}
public double nextDouble()
{
return Double.parseDouble(next());
}
public void
close() throws Exception
{
br.close();
}
}